M.Yas'ko "Numerical Method for Calculation of the Nonlinear Waves on Water of the Arbitrary Depth"

Numerical Method for Calculation of the Nonlinear Waves on Water of the Arbitrary Depth

M. Yas'ko

Dnipropetrovsk University, Mechanical and Mathematical Faculty,

320625, Dnipropetrovsk-10, Ukraine

Abstract

The numerical method is developed for calculation steady nonlinear water waves travelling over the free surface of an inviscid, incompressible fluid under the assumption of potential flow. The problem is treated as two dimensional for stream function of disturbed flow. The numerical model uses a boundary element method for discretization in space. For definition of the unknown free boundary an iterative procedure is proposed. This procedure is based on the solution of the third boundary problem on an each step. The features of the method are a comparatively small computational effort and enhanced efficiency and precision. For illustration, some computational results are presented for the shape and integral properties of the nonlinear periodic waves.

§1 Introduction

The two kinds of the numerical methods are used on the whole for the calculations of the nonlinear waves: Fourier series expansions [1] and boundary element method (BEM) for velocity potential [2,3]. In the present paper new formulation of the problem for the stream function are used. The formulation for the stream function leads to new linear boundary condition and makes lighter the solution of the nonlinear problem. The mathematical problem is formulated in §2. In §3 the method of calculation of nonlinear problem is described. The numerical results for shape and integral properties of waves are presented in §4.

§1 Problem definition

We consider a steady nonlinear waves, moving with speed U to the right, on the surface of a frictionless, irrotational, incompressible fluid of finite depth H , as a wave in figure 1. The free surface is at constant pressure, and has zero surface tension.

Figure 1. The definition sketch of the nonlinear wave.

We choose Cartesian coordinates connected with wave with the x-axis parallel to the bottom and the z-axis directly vertically upwards. We choose U as the unit of velocity and L=U²/2g as the unit of length. Thus the problem has one parameter - dimensionless depth h=2gH / U².

The governing equation for the 2D flows in dimensionless variables is

Δψ = 0 (1)
where ψ is the disturbed stream function (stream function in fixed coordinate system); the velocity in moving coordinate system (x,z) is

V_x=1+ψ_,z, V_z=-ψ_,x

The boundary conditions can be described in the following way. The kinematic condition on free surfaces (x(s), z(s)) and horizontal bottom is

V_n=-ψ_,s=0, (2)
where n is the unit outward normal vector,s is the unit tangential vector, s represents the curvilinear abscissae of the point on a free streamline. Equation (2) indicates that the flux through the boundary is zero. This equation can be integrated over the free streamline with the condition ψ(∞)=0 and it becomes

ψ(s)=z(s), (3)
The horizontal bottom is a streamline also on which we require ψ=0.

On the free surface, where a pressure is constant, the Bernoulli's equation yields

V_s² + z = 1,
where V_s=ψ_,n -x' is a tangential velocity on the free surface in the moving coordinate system. Then the dynamic boundary condition on the free boundary may be described in following manner

ψ_,n = x' - (1-z)^½, (4)
where s - is a curvilinear abscissae of the point on free streamline.

Thus, we have a classic free boundary problem: a location of the free streamline is unknown and two boundary conditions (3) and (5) are known on the free surface. For this problem, one parameter defines a unique solution: dimensionless depth h . For the nonlinear periodic wave two parameters define an unique solution: h and &\lambda;. Of course, we must denote that trivial solution ( ψ=0 and flat free surface) exists for any h and λ.

§3 Linear problem

In the case of the linear waves we can use (3) as follows

ψ_,n =½ ψ

(5)

Then the problem has ordinary solution

ψ = A(exp 2πyλ^-1 - exp 2π(2h-y)λ^-1) cos 2πxλ^-1

(6)

and

h =

λ
4π

log

λ+4π
λ-4π

(7)

From this equation it follows λ > 4π and h>2 , i.e. the dimension velocity of the periodic waves U < (gH)^½.

§3 Numerical method for nonlinear problem

Let be initial location of the free surface (x₀(s),z₀(s)) is known. Consider on the free surface the boundary condition of the third kind

ψ_,n = x'₀ - ½(2-z₀ - ψ) (1-z₀)^-½ = α ψ + β

(8)

where α and β are coefficients, depending upon shape of free surface.

The classic 'boundary element method' technique (see, Brebbia and others [4]) was used for the solution of the boundary problem of the third kind. In order to solve the problem of the free boundary, the shape of the free streamline must be calculated by successive iterations. The new location of the free surface is calculated by formula

z = γz₀ + (1-γ)ψ, (9)
where γ was in range [0,1], after that iterative cycle continued. If iteration process is coincided, then formula (8) translates in dynamic boundary condition (4). The iterative procedure is continued until a converge criterion is satisfied. Usually, 6÷15 iterations demanded for the coincidence. Number of iterations increased for highest waves to 40÷50.

§4 Numerical results

To demonstrate the numerical scheme developed above, we consider a 2D periodic wave. Irregular mesh of boundary elements was used with minimal elements near the wave crest. Number of boundary elements for the half of the wave was N=80 for all computations. The computations confirmed that nonlinear periodic waves exist for h>2.

For check of program, there was made the computations for waves of the small amplitude and there was made comparison with linear theory. Results are shown in figure 2.

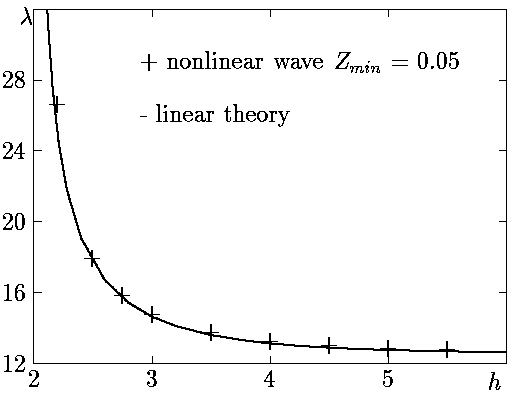Figure 2. Comparison wavelength for nonlinear waves with small amlitude and for linear theory.

The computed values of Z_max, Z_min, displacement S and wave length λ are shown in table 1 for the several depths h.

Table 1. Integral properties of the nonlinear waves.

h	Z_max	Z_min	λ	S
10	0.9801	-0.5617	10.853	-0.3977
10	0.9801	-0.5617	10.853	-0.3977
10	0.9020	-0.5804	11.005	-0.4074
10	0.9801	-0.5617	10.853	-0.3977
4	0.7897	-0.7001	13.264	-2.0297
4	0.5109	-0.5001	13.311	-0.9638
4	0.2989	-0.3000	13.254	-0.1543

An amplitude of the wave A=Z_max-Z_min. In the case of steady waves on deep water Williams [5] indicated an upper limit of A/λ=0.141063. In the peresent work this value was 0.142. The nonlinear computation confirmed the periodic nonlinear waves exist for h > 2.

In the figure 2 the dependence between λ and extremums of the wave Z_max and Z_min are presented for few depth.

Figure 3. Extremums of nonlinear waves.

In the case of shallow water ( h=2.5 ) wave length can be very large for not very high waves. It is a case of the cnoidal waves. For the intermediate depth ( h=4 ) wave length is almost constant for all waves. On the deep water the wave length is decreasing for the highest waves. The dependence (4) between the dimensionless depth h and wave length λ was right for the all waves with small amplitude.

§5 Conclusions

The basic principle of the boundary element method has been presented in this paper for the calculation of the solitary waves in nonlinear formulations. The advantage of this method is the simplicity of the boundary calculations in the physical plane. Comparisons with analytical and numerical data of other authors suggest that the solutions obtained by the present numerical method are quite accurate. The flow is especially well modeled in the case of the highest waves. Similar numerical technique could be used to investigation of the gravity-capillary and periodic nonlinear waves.

References

Rienecker, M.M., Fenton, J.D.: A Fourier approximation method for steady water waves. J. Fluid Mech., 1981, 104, 119-137.
Rottman, J.W., Olfe, D.B.: Numerical calculation of steady gravity capillary waves using an integro-differential formulation. J. Fluid Mech., 1979, 94, 777-793.
Cooker, M.J.: A boundary-integral method for water wave motion over irregular beds. Engng. Analysis with Bound. Elements, 1990, 7, No.4, 205-213.
Brebbia, C.A., Telles, J.C.F., Wrobel, L.C.: Boundary Element Techniques. Theory and Applications in Engineering, 1984, Springer-Verlag, Berlin and New York.
Williams, J.M.: Limiting gravity waves in water of finite depth Phil. Trans. Roy. Soc., London, ser. A 302, 139-188 (1981)