Numerical Method for Calculation of the Solitary
Waves on Water of the Arbitrary Depth
M. Yas'ko
Dnipropetrovsk University, Mechanical and Mathematical Faculty,
320625, Dnipropetrovsk-10, Ukraine
Abstract
A numerical method is developed for calculation steady nonlinear
water waves travelling over the free surface of an inviscid, incompressible
fluid under the assumption of potential flow.
The problem is treated as two dimensional for stream function
of disturbed flow. The numerical model uses a boundary element method for
discretization in space. For definition of the unknown free boundary
an iterative procedure is proposed. This procedure based on the solution
of the third boundary problem on an each step. The features of the method
is a comparatively small computational effort and enhance efficiency and
precision.
For illustration, some computational results are presented for the shape and
integral properties of the solitary waves.
§1 Introduction
Solitary waves in shallow water have been preoccupied since the classical
observations by Scott Russel in 1838. For reviews of modern numerical calculations
of this type of wave see surveys of Miles [1] and Schwartz and Fenton [2].
After that solitary waves in water of finite depth have also been calculated
by Hunter and Vanden-Broeck [3], and Tanaka [4]. The numerical calculations
of the nonlinear waves are based on two techniques:
- methods of a transformed plane, in which physical domain is conformally
mapped to a flat-bedded domain or to circle and
conformal mapping have been used for solution, in works of
Longuet-Higgins [5], Hunter and Vanden-Broeck[3], Tanaka[4];
- methods of a physical plane, in which boundary integral equations have been
solved numerically in physical plane. For example, Rottman and Olfe [6] used
boundary integral equation and Newton's iterative procedure for the solution
of nonlinear algebraic system, Rienecker and Fenton [7] used Fourier
expansion for this problem.
In the present work the direct boundary element method and new iterative procedure
have been used for the solution of the solitary wave problem.
The mathematical problem is formulated in §2, where an equation is written
for a stream function ψ in a physical plane. In §3 the method of
calculation of nonlinear problem is described.
The numerical results for shape and integral properties of solitary waves
are presented in §4.
§2 Problem definition
We consider a steady solitary wave, moving with speed U to the right, on
the surface of a frictionless, irrotational, incompressible fluid of finite
depth H, as in figure 1. The free surface is at constant pressure, and has
zero surface tension.
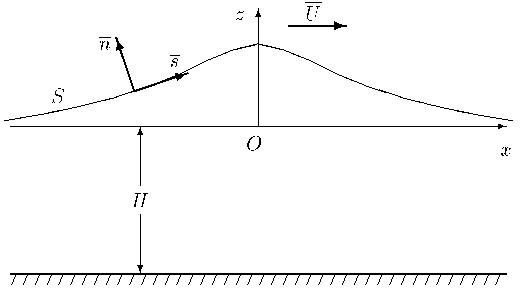
Figure 1. The definition sketch of the solitary wave.
We choose Cartesian coordinates connected with wave
with the x-axis parallel to the bottom and the z-axis directly vertically
upwards. The coordinate z is measured from the level of the free surface
at |x|=∞. There is a uniform gravitational field.
Acceleration of the gravity g is acting in the negative z-direction.
We choose U as the unit of velocity and L=U2/2g as the unit
of length. Thus the problem has one parameter - dimensionless
depth h=2gH / U2.
The governing equation for the 2D flows in dimensionless variables is
where ψ is the disturbed stream function (stream function in fixed
coordinate system); the velocity in moving coordinate system (x,z) is
The boundary conditions can be described in the following way.
As |x|–>∞, the flow is require to approach a uniform
stream with constant velocity U in x-direction and uniform
depth h.
The kinematic condition on free surfaces (x(s), z(s)) and horizontal
bottom is
where n is the unit outward normal vector,s is the
unit tangential vector, s represents the curvilinear abscissae of the point
on a free streamline. Equation (2) indicates that the flux through
the boundary is zero. This equation can be integrated over the
free streamline with the condition ψ(∞)=0
and it becomes
The horizontal bottom is a streamline also on which we require ψ=0.
On the free surface, where a pressure is constant, the Bernoulli's equation
yields
where Vs=ψ,n -x' is a tangential velocity on
the free surface in the moving coordinate system. Then the dynamic boundary condition
on the free boundary may be described in following manner
where s - is a curvilinear abscissae of the point on free streamline.
On the infinity
Thus, we have a classic free boundary problem: a location of the free streamline
is unknown and two boundary conditions (3) and (5) are known on the free
surface. For this problem, one parameter defines a unique solution:
dimensionless depth h . Of course, we must denote that trivial solution
( ψ=0 and flat free surface) exists for any h.
§3 Numerical method
Let be initial location of the free surface (x0(s),z0(s))
is known.
The boundary integral representation of solution of the equation
| ½ψ = ∫S (ψP,nGMP
-ψPGMP,n) dSP |
(7) |
where GMP=FMP-FLP
is a Green's function for half-plane;
M(x,z) and P(ξ,η) are points on the boundary, L(x,-2h-z) is a
point symmetric M relatively bottom plane;
FMP = -(2π)-1 ln rMP is a fundamental solution
of the Laplace equation for infinity isotropic 2D medium; rMP
is a distance between points M and P.
Consider on the free surface the boundary condition of the third kind
| ψ,n = x'0 - ½(1-z0)-½(2-z0-ψ)
= αψ+β,
|
(8) |
where α and β are coefficients, depending upon shape of free surface.
The discretization of (7), which leads to the classic "boundary element
method" technique (see, Brebbia and others [8] is described below. In the
boundary element method, the above integral equation is solved numerically
by dividing the boundary S into N boundary elements, in each of which
ψ and ψ,n are approximated by constants. We
denote these values by ψi and ψi,n, i=1,…N;
and apply equation (8) at one nodal point Mi in the center of each
boundary element to obtain
| Aij=∫SjGij,ndSP |
Bij=-∫SjGijdSP |
where ∫Sj denotes integration over the j-th boundary
element. Here and what follows the summation over repeating indices is assumed.
Coefficients Aij and Bij of the linear system of
equations (9) are integrated analytically over boundary elements using
the analitical formulas.
Eliminating the ψi,n from each elements on the free surface
by applying the boundary condition (8) in each nodal point,
we thus obtain a system of N linear algebraic equations with
N unknown ψi
|
(Aij αj + Bij - ½δij) ψj=
- Aij ψj
| (10) |
where δij is the Kroneker delta. The system of N
linear algebraic equations (10) was solved by the direct Gaussian
elimination method.
In order to solve the problem of the free boundary, the shape of the
free streamline must be calculated by successive iterations. The new location of the
free surface is calculated by formula
after that iterative cycle continued. If iteration process is coincided,
then formula (8) translates in dynamic boundary condition (5). The
iterative procedure is continued until a converge criterion is satisfied.
Usually, 15÷30 iterations demanded for the coincidence. Number of
iterations increased for highest waves to 40÷50.
On the free boundary,
the velocity component normal to the free surface will be zero only
at the convergence of the iterative process. After finishing the
iterative process , the maximum height of wave and other characteristics
have been defined as a function of dimensionless depth h.
§4 Numerical results
Number of boundary elements for the half of the wave was N=80 for all
computations. Initial approximation of the free streamline calculated
by formula
where a=2.0-h and c=0.667a½.
To demonstrate the numerical scheme developed above, we consider a 2D
solitary wave. The computations showed that solitary waves exist for h
in range from 2.0 to 1.1895.
The computed profiles of the free surface are presented in figure 2 at the
values of h=1.8, 1.6, 1.4 and 1.19 (curves 1, 2, 3 and 4 accordingly). In case
h=1.8 we have a gently sloping solitary wave. In case h=1.19 we have a
solitary wave nearly to maximum height. In this case the numerical method
gives sharper angle at the crest ~120°.
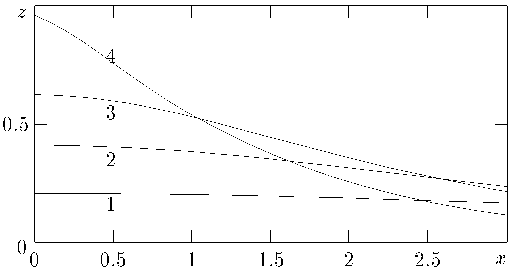
Figure 2. Profiles of the solitary waves.
The highest wave had been computated at h=1.1895 and her
amplitude was Zmax=0.981. Extrapolation for Zmax=1
gave value hmin=1.189.
In table 1 the ratio Zmax compared with data of other authors.
Table 1. Comparison of maximum wave height with data of other authors.
| works | zmax/hmin |
| Lenau [9] | 0.827 |
| Longuet-Higgins and Fenton [10] | 0.827 |
| Yamada and others [11] | 0.8262 |
| Witting [12] | 0.8332 |
| Cooker [13] | 0.83 |
| present work | 0.841 |
Thus, we can say that velocity of solitary waves may be in range
(gH)½ ÷ 1.3(gH)½.
The trajectory of point on the free boundary are presented in figure 3 for
solitary waves shown in figure 2. To calculate the trajectory of a surface
fluid particle we find its velocity and integrate by the time-stepping
algorithm of two order.
Denote that this curves are very similar cycloids.
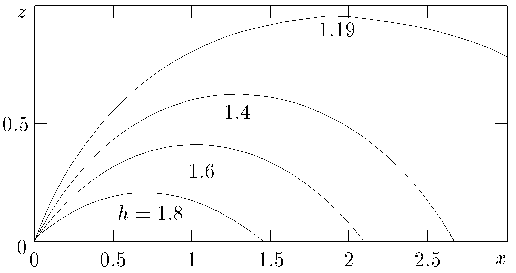
Figure 3. Trajectories of the point on the free surface.
Now we shall consider some integral quantities of the solitary wave relative
to fixed coordinate system. Firstly, we may define net displacement, or excess
mass
We may define the dimensionless gravitational potential energy
and the kinetic energy of the relative motion, which can be written using
Green's theorem as follows
The computed values of Zmax, Ek, Ep and S are
shown in table 2.
Table 2. Calculated integral properties of solitary waves.
| h | zmax | EK | EP
| S |
| 1.90 | 0.1041 | 0.0339 | 0.0668 | 1.9805 |
| 1.80 | 0.2047 | 0.0911 | 0.1757 | 2.6380 |
| 1.70 | 0.3062 | 0.1595 | 0.3009 | 3.0266 |
| 1.60 | 0.4092 | 0.2335 | 0.4304 | 3.2461 |
| 1.50 | 0.5143 | 0.3084 | 0.5549 | 3.3524 |
| 1.40 | 0.6243 | 0.3795 | 0.6658 | 3.3495 |
| 1.30 | 0.7438 | 0.4410 | 0.7525 | 3.2433 |
| 1.22 | 0.8637 | 0.4747 | 0.7889 | 3.0505 |
| 1.21 | 0.8838 | 0.4767 | 0.7891 | 3.0131 |
| 1.20 | 0.9093 | 0.4773 | 0.7866 | 2.9658 |
| 1.19 | 0.9575 | 0.4730 | 0.7745 | 2.8835 |
The wave amplitude Zmax, potential and kinetic energy and also
displacement S are presented in
figure 4 as a functions of dimensionless depth h (curves 1, 2, 3 and 4
accordingly).
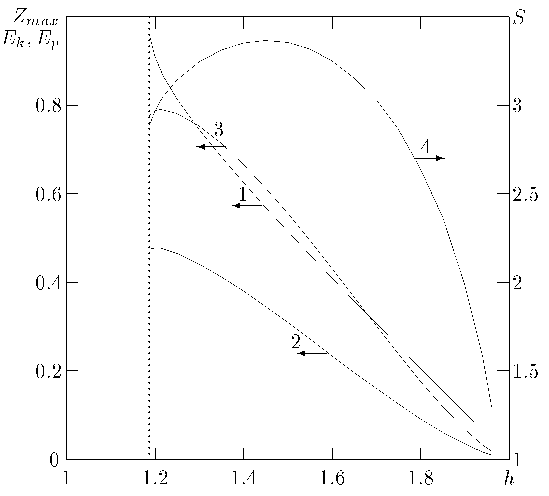
Figure 4. Integral propeties of the solitary waves.
If h is decreased than amplitude Zmax of the solitary
wave is increased right up to 1 for h=1.189. In range 1.3 < h < 2
the amplitude Zmax change nearly linearly and solitary
waves can be accurately approximated by solutions to the Kortveg-de Vries equation.
Other functions is changed nonmonotonically
with h, but the potential energy always exceeds the kinetic.
§5 Conclusions
The basic principle of the boundary element method has been presented in
this paper for the calculation of the solitary waves in nonlinear formulations.
The advantage of this method is the simplicity of the boundary calculations
in the physical plane. Comparisons with
analytical and numerical data of other authors suggest that the solutions
obtained by the present numerical method are quite accurate. The flow is
especially well modeled in the case of the highest waves.
Similar numerical technique could be used to investigation of the
gravity-capillary and periodic nonlinear waves.
References
-
Miles, J.W.: Solitary waves. Ann. Rev. Fluid Mech.,
1980, 12, 11-23.
-
Shwartz, L.W., Fenton, J.D.: Strong nonlinear waves.
Ann. Rev. Fluid Mech., 1982, 14, 39-60.
-
Hunter, J.K., Vanden-Broek, J.M.: Solitary and periodic gravity-capillary
waves of finite amplitude. J. Fluid Mech., 1983, 134, 205-219.
-
Tanaka, M.: The stability of solitary waves. J. Phys. Fluids,
1986, 29, 650-655.
-
Longuet-Higgins, M.S.: Limiting forms for capillary-gravity waves.
J. Fluid Mech., 1988, 194, 351-375.
-
Rottman, J.W., Olfe, D.B.: Numerical calculation of steady gravity
capillary waves using an integro-differential formulation.
J. Fluid Mech., 1979, 94, 777-793.
-
Rienecker, M.M., Fenton, J.D.: A Fourier approximation method for
steady water waves. J. Fluid Mech., 1981, 104, 119-137.
-
Brebbia, C.A., Telles, J.C.F., Wrobel, L.C.: Boundary Element
Techniques. Theory and Applications in Engineering, 1984,
Springer-Verlag, Berlin and New York.
-
Lenau, C.W.: The solitary wave of a maximum amplitude. J. Fluid Mech.,
1966, 26, 309-320.
-
Witting, J.: On the highest and other solitary waves. SIAM. J. Appl.
Math., 1975, 28, 700-719.
-
Yamada, H., Kimura, G., Okabe J.I.: Precise determination of the
solitary wave of extreme height on water of a uniform depth. Rep. Res.
Inst. Appl. Mech. Kyushu Univ., 1968, 16, 15-32.
-
Longuet-Higgins, M.S., Fenton, J.D.: On the mass, momentum, energy
and circulation of a solitary wave. II. Proc. R. Soc. London, Ser. A,
1974, 340, 471-493.
-
Tanaka, M.: The stability of solitary waves. Phys. Fluids, 1986,
29, 650-655.
-
Cooker, M.J.: A boundary-integral method for water wave motion over irregular
beds. Engng. Analysis with Bound. Elements, 1990, 7, No.4, 205-213.
-
Tanaka, M., Dold, J.W., Lewy M. and Peregrine, D.H. Instability and
breaking of a solitary wave. J. Fluid Mech., 1987, 185, 235-248.
-
Davis, R.E. and Acrivos, A. Solitary internal waves in deep water.
J. Fluid Mech., 1967, 91, 167-180.




