Numerical Method for Calculation of the Planar and Axisymmetric
Cavitational Flows
M. Yas'ko
Dnipropetrovsk University, Mechanical and Mathematical Faculty,
320625, Dnipropetrovsk-10, Ukraine
Abstract
The numerical algorithm is proposed for calculation of the steady cavitating
flows around the arbitrary plane and axisymmetric blunt-ended bodies with the
fixed separation point. The fluid is assumed as incomressible and weightless,
and the flow is assumed as potential. For description of the cavitational flow
the Riabouchinsky cavitating scheme ("with the mirror") was used and the length
of the free streamline was chosen as a parameter.
For definition of the unknown free boundary the iterative procedure is
proposed. This procedure is based on the solution of the linear boundary
problem on an each step.
Numerical results for the drag coefficient, the shape of cavities and cavitation
numbers are presented for cavitating flows behind the cones and wedges with
halh-angle in range [10°,120°]. These results are compared with the data
of other authors for the disk (90°) and cones.
§1 Introduction
The tasks of designing the high speed submarine apparatus and predicting their
performance have preoccupied engineers for many years. Although thera are only a
small number of the numerical axisymmetric fully cavitating flows calculation
methods. The numerical calculations of axisymmetric cavitating flows are based
on two techniques:
-
finite difference method proposed by Brennen [1]. The solutions are obtained
for cavities behind a disk and a sphere in different zise of solid wall tunnel.
The same problem was also treated by Garabedian [2], who appoached the axisymmetric
case by the successive correction involving the solutions of a linear mixed
boundary-value problem.
-
boundary integral equation methods in works Amromin and Ivanov [3], Gyzevsky [4],
Kojoro [5] and Wrobel [6].
These papers present the formulations of the boundary element method (BEM) for
solution of axisymmetric cavity flow problems.
The governing equation is written in terms of Stokes' stream function,
requiring a utilization of infirect BEM or, for direct BEM case, a new
fundamental solution to be found.
In present work the new numerical iterative algorithm based on direct boundary
element method (DBEM) is proposed for computation of the cavitational flows.
The mathematical problem is formulated in §2. In §3 the method of
calculation of nonlinear problem is described.
The numerical results are presented in §4.
§2 Problem definition
Cavitating flow around an axisymmetric body is generally a three-dimensional
problem. If the case is limited to zero angle of attack, this problem may be
described in the same manner as a two-dimensional problem.
The uniform stream with the velocity U0 flows round the blunt-ended
body shown in figure 1. Axis Oz ia a line (in planar case plane) of a symmetry.
The line OA ia a wetted surface of a body and AK is a free streamline. The line
KQ is a plane symmetry of the Ryabouchynsky flow. The positions of the boundaries
AK and KQ as well as the shape of the cavity are initially unknown.
Figure 1. The definition sketch of the cavitational flow.
We choose U as the unit of velocity and R as the unit of length.
The governing equation for the planar and axysymmetric potantial flow in dimensionless
variables is
where φ is the disturbed velocity potential; the velocity in the coorfinate
system (r,z) is
The boundary conditions can be described in the following way.
The kinematic condition on the wetted and free surfaces is
where n is the unit outward normal vector.
Equation (2) indicates that the flux through the boundary is zero.
Assuming uniform cavity pressure, on free streamline is valid the dynamic condition
where Uc is a constant velocity on free streamline;
s is the unit tangential vector, s represents the curvilinear
abscissae of the point on a free streamline.
On tline of symmetry KQ
The equation (3) can be integrated over the free streamline with the
condition (4) and it becomes
and it becomes
| ψ(s) = zK - z(s) + Uc (s-s*), |
(5) |
where s* is arclength of the free streamline.
For Riabounchunsky model, one dimensionless parameter defines a unique solution:
-
cavitation number
|
σ = | p0- pc
½ρU² |
= | Uc²
U0² |
- 1, |
where p0, pc are the remote upstream and cavity pressures
and ρ is the density of fluid;
-
or half-length of cavity
zL=zK-zA;
-
or arclength of the free streamline s*.
In the present work the arclength of this curve was chosen arbitrary as input data.
Thus, we have a classic free boundary problem: a location of the free streamline
is unknown and two boundary conditions (2) and (5) are known on the free
surface. For this problem, one parameter defines a unique solution:
s*.
§3 Numerical method
Let be initial location of the free streamline is known.
The boundary integral representation of the equation (1) is [8]
|
½φM = ∫S [φP,n(FMP-FLP)
- φP(FMP,n-FLP,n)]ρkdsP |
(6) |
where k=0 for planar case and k=1 for axisymmetric case; M(r,z) and P(ρ,ζ)
are points on the boundary; L(r,2zk-z) is a point symmetric relatively
plane KQ;
is a fundamental solution for isotropic 2D medium;
| FMP = π-1[(ρ+r)²+(ζ-z)²]-½ K(γ) |
is a fundamental solution for axisymmetric case;
| γ² = 4ρr[(ρ+r)²+(ζ-z)²]-½ |
rMP is distance between points M(r,z) and P(ρ,ζ).
In axisymmetric case, the complete elliptic integrals of the first K(γ)
and second kinds may be approximated by polynomial approximations [8]. In this
equation, the integrals are considered logaripthm singularuty when P tends towards M.
The discretization of (6), which leads to the classic 'boundary element
method' technique (see, Brebbia and others [9]) are discribed below.
In the boundary element method the integral equation is solved numerically
by dividing the boundary S into N+L elements (N boundary elements on the free
boundary and L on the wetted surface of the body), in each of wich φ and
φ,n are approximated by constants. We denote these values by
φi and φi,n, i=1,…N+L; and apply equation
(6) at one nodal point Mi in each boundary element to obtain
| ½φi = |
N+L
Σ
j=1 |
(φj,n ∫Sj GiPdsP -
φj ∫Sj GiP,ndsP), |
(7) |
where Sj denotes integration over jth boundary element.
In planar case the coefficients of the linear system of equation (7) integrated
analytically over intervals. In axisymmetric case numerical integration are
used over the boundary element, parametrising this interval in an appropriate
manner and taking into account the singularity in the intevals when i=j.
Eliminating the φi fromeach element on the free streamline and
φi,n from each element on the wetted boundary by applying the
corresponding boundary condition in each nodal point, we thus obtain a system
of N+L simultaneous linear algebraic equations with N+L+1 unknowns (
N unknowns φi,n on free boundary,
L unknowns φi on body boundary and value of velocity on free
streanline Uc. Additional equation for Uc we obtain by
equating value of potential in the separation point, calculated in (5) and
value obtained by linear extrapolation by two points on the wetted surface
| zK - zA - Ucs* =
φN+1 + (φN+1-φN+2) |
ΔN+1
–––––––––
ΔN+1+ΔN+2 |
(8) |
where Δi is the length of the jth boundary element.
The system N+L+1 linear algebraic equations (7,8) was solved by the direct
Gaussian elimination method.
In order to solve the problem of cavitating flow, the shape of the cavity
must be obtained by successive iterations. The new location of the free
boundary have been calculated by integration
| r'new = - φ,n
[φ,n²+z'²]-½ |
(9) |
with initial condition r(0)=R, z(0)=ZA. If iterative process is
coincided, then formula (9) translates in kinematic condition (2). The
iterative procedure is continued until a converge criterion is satisfied. Usually,
6÷12 iterations demanded for the coincidence. On the cavity surface,
the velocity component normal to the boundary will be zero only at the end of
convergence of the iterative process. After finishing the iterative process,
the cavitation number σ must be retained as a solution parameter.
§4 Numerical results
To demonstrate the numerical scheme developed above, we consider a planar
cavitational flow behind the wedges and plate. This problem has analytical
solution in complex variables (see, Riabouchinsky [7]). Comparison of numerical
results for planar flow (65 boundary elements) and analytical data made in table 1.
Table 1. Comparison of numerical and analytical results for plate and wedge.
| α° | σ |
RK/R |
cd |
zL/R |
| calc. | anal. |
calc. | anal. |
calc. | anal. |
| 90 | 0.45 | 3.491 | 3.4847 | 1.2808 | 1.2788 | 15.58 | 15.568 |
| 90 | 0.30 | 4.727 | 4.7305 | 1.1470 | 1.1451 | 31.74 | 31.798 |
| 90 | 0.10 | 12.07 | 12.201 | 0.9644 | 0.9680 | 243.3 | 245.68 |
| 45 | 0.30 | 3.441 | 3.4540 | 0.8360 | 0.8361 | 22.88 | 23.941 |
Here α is half-angle of wedge (α=90° corresponds by the plate).
The differences between calculated and analytical values are very small.
For axisymmetric case numerical values cd*=Fd/πRK²
for cones are compared with the numerical data of Guzevsky [4] in table 2.
Coincidence between data of Guzevsky [4] and present work is close also.
Table 2. Comparison of numerical Cd* with data of Guzevsky [4] (σ=0.25)
| α° | 90 |
60 | 30 |
| Guzevsky [4] | 0.223 | 0.223 | 0.224 |
| present work | 0.2186 | 0.2198 | 0.2207 |
The computed and experimentally observed (Brennen [1]) position of the free
streamline behind the disk are presented in figure 2 for cavity number
σ=0.2.
Figure 2. Comparison of theoretical and experimental cavity
profiles for disk (σ=0.2), + Brennen [1].
The agreement of these data is very close. The pressure distribution on the wetted
surface of disk for σ=0.24 has been presented in figure 3. There is close
agreement with the experimental data of Rouse and McNown from [1].
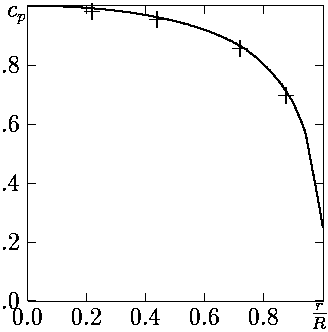Figure 3. Pressure distribution on surface of disk (σ = 0.24),
experimental data + for σ=0.24 from [1]).
The dependencies of drag coefficient cd and cavity radius RK
are presented in figure 4 for cavity number σ=0.1. Here the value
α=90° corresponds by the disk.
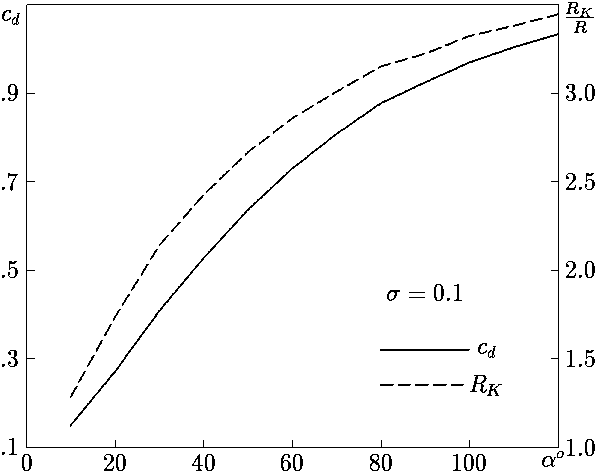Figure 4. Variation of drag coefficient and cavity radius
with half-angle of cone for σ=0.1.
§5 Conclusions
The boundary element method has been presented in
this paper for the computation of the planar and axisymmetric cavitational
flows in non-linear formulation. Comparisons with analytical, numerical and
experimental data suggests that the solutions obtained by the present numerical
method are quite accurate. The flow is partially well modelled in the case of
blunt-ended bodies with fixed separation point, namely as disk.
References
-
Brennen, C.A. Numerical Solution of Axisymmetric Cavity Flows
J. Fluid Mech.., 1969, 37, p.4, 671-688.
-
Garabedian, P.R. The Calculation of Axially Symmetric Cavities and Jets
J. Math.., 1955, 6, 777-793.
-
Amromin, E.L. and Ivanov, A.N. Axisymmetric flows round bodies in regime
of the developed cavitation
Izv. Sov. Acad. Sci. Mech of Fluid and Gas, 1975, N.3, 37-42.(in Russian)
-
Guzevsky, L.G. Numerical analysis of cavitational flows
Sub. Div. of Sov. Acad. Sci. In-t Thermophysics Preprint 40, 1979. (in Russian)
-
Kojoro, L.A. Calculation of Axisymmetric Stream Flows Round of the Bodies by
Ryabouchinsky scheme
Sci. Notes of CAHI 1980, 11, 109-115. (in Russian)
-
Wrobel, L.C. Numerical solution of axisymmetric cavity flows using the
boundary element method.
Int. J. Numer. Methods Fluids 1993, 16, No.9, 845-854.
-
Riabouchinsky, D. On Steady Fluid Motion with Free Surface
Proc. Lod. Math. Soc., 1920, 19, 202-212.
-
Abramovitz, M. and Stegun, I.A. (Eds) Handbook of Mathematical Functions
New York: Dower, 1974.
-
Brebbia, C.A., Telles, J.C.F., Wrobel, L.C.: Boundary Element
Techniques. Theory and Applications in Engineering, 1984,
Springer-Verlag, Berlin and New York.